Matlab'da yapılan bir YSA ile XOR uygulaması daha önceden paylaşmıştım. Şimdi de başka bir örnek paylaşmak istedim. Matlab'da YSA uygulaması yapan arkadaşlara faydalı olması dileğiyle...
ÖZEL VEYA (XOR) problemi sahip olduğu doğrusal olmayan yapı sayesinde sınıflama ve modelleme algoritmalarının test edilmesi ve başarılarının ölçülmesinde önemli bir ölçüt haline gelmiştir. Doğruluk tablosu Tablo 1.1’de verilmiştir. Bu şekilden de anlaşılabileceği gibi basit bir doğru ile lojik 1 ve lojik 0 olan değerleri birbirlerinden ayrıştırılamamaktadır. Oysaki diğer lojik operatörler örneğin VE (AND), VEYA (OR) gibi işlemler bir doğru ile kolaylıkla sınırlanabilmektedir.
Tablo 1.1. XOR lojik operatörünün doğruluk tablosu
|
A |
B |
Y= A XOR B |
Y= A OR B |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
- a) XOR operatörü b) OR operatörü
Xor problemi için hata 0,03 ,lamda değeri 0,5 seçilmiştir . Problemin Matlab kodu şu şekildedir :
Aşağıdaki matlab kodları XOR problemi için bir çözüm sunar. XOR problemi, iki girdinin XOR mantıksal işlemi sonucunda elde edilen çıktıyı tahmin etmekle ilgilidir. Bu nedenle, verilen girdilerin doğru çıktılarını (beklenen değerler) öğrenen bir sinir ağı modeli kullanarak XOR problemini çözmeye çalışır. Bu kod, bir üç katmanlı sinir ağı modeli kullanarak XOR problemini çözmek için geri yayılım algoritmasını uygular.
XOR Probleminin M-File Kodu:
input = [0 0; 0 1; 1 0; 1 1]; %giriş matrisi
output = [0;1;1;0]; %beklediğimiz değerler
bias = [-1 -1 -1]; %bias değerleri
hata=0.03;
lamda =0.5;
Ht =zeros(1,500);
m=1;
x=true;
t=0; %iterasyon sayıcı
weights = [0.341332 0.129952 0.570345 ;-0.115223 -0.923123 0.328932 ;-0.993423 0.164732 0.752621 ];
%w(1,1)-w(2,1)-w(3,1) eşik değerleri ,
%w(1,2)-w(1,3)-w(2,2)-w(2,3)girdi ağırlıkları,
%w(3,2)-w(3,3) ara katman ağırlıkları
while(x)
if(0.03<=hata)
out = zeros(4,1);
numIn = length (input(:,1)); %girişin satır sayısı
for j = 1:numIn
H1 = bias(1,1)*weights(1,1) + input(j,1)*weights(1,2)+input(j,2)*weights(1,3);
x2(1) = 0.5* (1+H1/(1+abs(H1)));
H2 = bias(1,2)*weights(2,1)+ input(j,1)*weights(2,2) +input(j,2)*weights(2,3);
x2(2) = 0.5* (1+H2/(1+abs(H2)));
x3_1 = bias(1,3)*weights(3,1) + x2(1)*weights(3,2) +x2(2)*weights(3,3);
out(j) = 0.5* (1+x3_1/(1+abs(x3_1)));
delta3_1 = out(j)*(1-out(j))*(output(j)-out(j));
delta2_1 = lamda*x2(1)*(1-x2(1))*weights(3,2)*delta3_1;
delta2_2 = lamda*x2(2)*(1-x2(2))*weights(3,3)*delta3_1;
for k = 1:3
if k == 1 % Bias
weights(1,k) = weights(1,k) + lamda*bias(1,1)*delta2_1;
weights(2,k) = weights(2,k) + lamda*bias(1,2)*delta2_2;
weights(3,k) = weights(3,k) + lamda*bias(1,3)*delta3_1;
else % k=2 or 3 input,
weights(1,k) = weights(1,k) + lamda*input(j,1)*delta2_1;
weights(2,k) = weights(2,k) + lamda*input(j,2)*delta2_2;
weights(3,k) = weights(3,k) + lamda*x2(k-1)*delta3_1;
end
end
end
Ht(1,m)= abs(output(j)-out(j));
hata=Ht(1,m);
t=t+1;
m=m+1;
end
if(0.03>hata)
x=false;
end
end
figure(1)
plot(Ht(1,:),'r');
figure(2)
plot(output(:,1),'r')
hold on
plot(out(:,1),'b')
Bu kodlar, bir yapay sinir ağı (YSA) modelinin eğitilmesi için kullanılır. Bu YSA, bir giriş matrisi (input) ve beklenen çıktı değerleri (output) arasındaki ilişkiyi öğrenir.
Kodlar, üç katmanlı bir YSA modeli kullanır. İlk katman, giriş verilerini ve ağırlıklarını içerir. İkinci katman, gizli katmandır ve girdileri işler. Üçüncü katman, çıkış katmanıdır ve modelin tahmin ettiği çıktı değerlerini üretir. Kodlar, iteratif bir öğrenme algoritması olan geri yayılımlı (backpropagation) algoritmasını kullanarak YSA modelinin ağırlıklarını günceller. Bu algoritma, çıktı hatalarının geriye doğru yayılması ve her bir ağırlığın hataya katkısının hesaplanması yoluyla çalışır. Ayrıca, hata seviyesi (hata) belirlenen bir eşik değerine (0.03) eşit veya daha az olana kadar her bir öğrenme iterasyonu (epoch) için hesaplanır. Epoch sayısı (t) da takip edilir ve hata seviyesi belirlenen eşik değerine ulaşıldığında öğrenme döngüsü sonlandırılır.
Son olarak, yazdığım Matlab kodları, her bir epoch'ta elde edilen hata değerlerinin (Ht) bir histogramını çizer ve beklenen çıktı değerleri (output) ile YSA modeli tarafından tahmin edilen çıktı değerlerinin (out) bir grafiğini çizer. Bu grafiğin mavi çizgisi, YSA modelinin tahminlerini gösterirken kırmızı çizgi, beklenen çıktı değerlerini gösterir.
M-File Kodunun Çıktısı
Hata değerlerinin matlab çıktısı Şekil 1.1 de verilmiştir. Hata 0,03 , İterasyon sayısı 55626’dır.
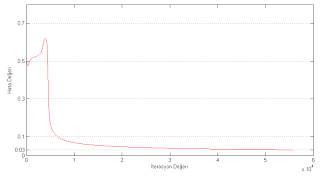
Şekil 1.1. Hata değerinin çıktısı
Beklenen çıktı ile sistemin çıktısının aynı grafikte gösteren matlab çıktısı Şekil 1.2’te verilmiştir.
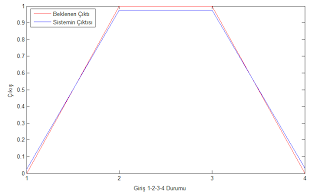
Şekil 1.2. Beklenen çıktı ve sistem çıktısının grafiği
Matlab koduna göre ağın verdiği çıkış ve hata değerleri Tablo 1.2’de gösterilmiştir.
Tablo 1.2. XOR problemini öğrendikten sonra ağın ürettiği çözümler ve hata oranları
|
Durumlar |
Girdi 1 |
Girdi 2 |
Beklenen Çıktı |
ÇIKIŞ(OUTPUT) |
Hata |
|
1 |
0 |
0 |
0 |
0,025727 |
-0,025727 |
|
2 |
0 |
1 |
1 |
0,974568 |
0,025432 |
|
3 |
1 |
0 |
1 |
0,974217 |
0,025783 |
|
4 |
1 |
1 |
0 |
0.029999 |
-0,029999 |
'ysa, matlab, 'matlab ysa', 'yapay sinir ağları', 'ysa ile denklem çözümü', 'ysa 2 bilinmeyenli denklem', 'yapay sinir ağları 3 bilinmeyenli denklem, 'Geri Yayılım Yöntemi', 'Newton Yöntemi', 'Levenberg-Marquardt metodu', 'matlab ysa uygulamaları', 'yapay zeka', 'ysa uygulaması', 'artificial neual networks', 'or kapısı ve ysa', 'or gate ysa', 'veya kapısı matlab', 'or gate veya kapısı', 'ysa ile hava sıcaklığı', 'ysa ile tahmin', 'and kapısı ve ysa', 'and gate ysa', 've kapısı matlab', 'and gate ve kapısı', 'xor kapısı ve ysa', 'xor gate ysa', 'özel veya kapısı matlab', 'xor gate özel veya kapısı','iki girişli tek çıkışlı', 'sinüsoidal fonksiyon', 'sinüzoydal fonksiyon ysa matlab', 'iki giriş tek çıkışlı sinüsoidal fonksiyonun ysa uygulaması', 'matlab uygulamaları', 'ysa uygulamaları', 'yapay sinir ağı uygulamaları', 'Ali Osman Gökcan', 'Ali Osman Hoca', 'Ali Osman', 'ali osman matlab', 'ysa ile dc motor kontrolü'
--->>> YSA ile OR Kapısı Problem Çözümü için TIKLAYINIZ <<<---
--->>> Matlab'da Analitik Yöntem & Euler Metodu karşılaştırması için TIKLAYINIZ <<<---
--->>> YSA ile AND Gate Matlab Çözümü için TIKLAYINIZ <<<---
